鱼书学习笔记

Once a new technology rolls over you, if you’re not part of the steamroller, you’re part of the road. ― Stewart Brand.

第一章 Python 入门

见 Python 笔记

广播

在矩阵运算中，广播（Broadcasting）是一种强大的机制，它允许NumPy用不同大小的数组进行算术运算。在不明确的复制数据的情况下，广播提供了一种便捷的方式来扩展数组的维度。

广播规则如下：

1. 如果两个数组的维数不同，在较维度高的数组中，维度大小为1的地方会扩展为与另一个数组对应的维度大小。
2. 两个数组在对应的维度上，如果一个数组的维度大小为N，另一个数组的维度大小为1，或者缺失（即该维度不存在），则沿着该维度复制数组以匹配维度大小。
3. 如果两个数组在某个维度上不满足上述规则，则会引发错误。

第二章 感知机

感知机（perceptron）是由于美国学者 Frank Rosenblatt 在 1957 年提出，它是神经网络（深度学习）的起源算法。学习感知机的构造也是学习通向神经网络深度学习的一种重要思想。

感知机是一种简单的线性二分类模型，它是深度学习的基础构件之一。深度学习，特别是卷积神经网络（CNNs）和多层感知机（MLPs）是由多个类似于感知机的单元组成的。

基本概念：

感知机模型由一个输入层和一个输出层组成，其中输出层只有一个神经元。它用于对输入数据进行二分类。一个最简单的例子是一个单层单个两个输入信号和一个输出信号的感知机。

示意图如下图所示，其中 $x_1， x_2$ 是输入（信号），$y$ 是输出信号，$w_1,w_2$ 是权重（weight），而圆圈被称为”神经元”或者”节点”。输入信号被送往神经元后，会被分别乘以固定的权重，神经元会计算传送过来的信号的总和，只有当这个总和超过了某个界限值时，才会输出1，这被称为”神经元激活”，这个界限值被称为阈值，用符号 $\theta$ 表示

而这一过程可以用数学公式来表示：

通过合理设置权重和偏置，可以实现对输出的快速判断，得到想要的输出，也有些地方把权重和偏置统称为权重。 值得注意的是，这里权重和偏置虽然对结果的影响是相同性质的，但是他们的作用是不同的，就如同调整 pid 时根据反馈可以看到同样或类似的效果，但他们代表的含义不同：具体地说，权重是控制输入信号重要程度的参数，而偏置是调整神经元被激活的容易程度的参数。

通过这种方式，可以轻松实现逻辑门，但这时也会遇到问题：

根据数学表达式明显可知，这是一个线性函数把值域划成两个区域，以此达到分类的效果，但既然是线性的，他就只能实现非常简单的线性二分，但大多数时候空间（特征空间或决策空间）内数据的分类分布远比这要复杂，并不是一维可以适用判断的，比如异或门。

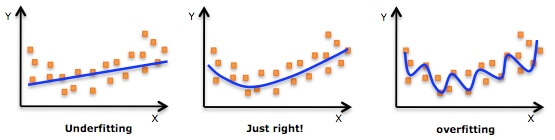
幸运的是，在数字电路系统中我们学过，由或非门或与非门的排列组合可以实现任意的别的门电路，所以我们只需要使用某一种基础单元，最终也可以组成复杂的结构，同样的，我们用若干层的单一门电路，也可以实现复杂功能。同理，对于感知机来说，多层的感知机可以实现执行更多复杂功能（以至于任何功能！）。例如我们将一个/单层感知机视为一个线性函数（好像后面有ReLu的说法），而多个/多层的感知机就相当于数层线性函数的叠加，而线性函数的层数（段数）越多，就能拟合越复杂的函数曲线。

有关感知机的一些关键概念（不止感知机）：

1. 基本单元：在深度学习中，每个神经元（或称为单元）通常执行一个简单的线性函数，然后通过一个非线性激活函数。这与单个感知机的操作非常相似。
2. 多层结构：深度学习模型之所以“深度”，是因为它们由多个层次的神经元组成，每一层都建立在前一层的输出之上。这种多层结构允许模型学习数据的复杂表示。
3. 参数共享：在卷积神经网络中，虽然感知机的概念被扩展到具有多个滤波器的卷积层，但每个滤波器本身可以看作是一个带有权重和偏置的感知机，它们在整个输入特征图上滑动以提取特征。
4. 特征学习：深度学习模型通过堆叠多个感知机层来学习从原始数据到高级特征的映射。底层可能学习边缘等简单特征，而高层可能学习更复杂的形状或对象特征。
5. 非线性激活：虽然感知机本身是线性的，但深度学习模型中的每个神经元通常包含一个非线性激活函数，如ReLU、Sigmoid或Tanh。这些非线性函数允许模型学习非线性决策边界。
6. 前馈和反馈：在深度学习中，信息通常以前馈的方式流动，从输入层通过多个隐藏层传递到输出层。然而，在某些类型的深度学习模型中，如循环神经网络（RNNs），信息也可以以反馈的形式流动。
7. 训练过程：深度学习模型通过反向传播算法进行训练，该算法计算损失函数关于模型参数的梯度，并使用这些梯度来更新模型的权重和偏置。
8. 泛化能力：通过组合大量的感知机单元，深度学习模型能够捕捉数据中的复杂模式，并在许多任务中展现出强大的泛化能力。

第三章 神经网络

感知机原始但强大，即便面对非常复杂的函数，多层堆叠的感知机也有能够把它表示（拟合）出来的可能性，那么代价是什么呢？代价就是每一层的感知机参数，目前都还是人为手动设定的。也就是说，虽然感知机的潜力是无限的，但人的精力是有限的

神经网络就是来解决这一问题的，在这一章节中会探讨神经网络如何从数据中学习权重参数

---

神经网络

感知机可以被视为神经网络的一个特例，是构成神经网络的基本单元。神经网络通过堆叠多个感知机（神经元）和层来构建复杂的模型，从而实现对复杂数据和任务的处理。

如下图是一个基本的神经网络模型：

我们把最左边的一列称为输入层（Input Layer），最右边的一列称为输出层（Output Layer）中间的就是中间层（Middle Layer），也叫隐藏层（Hidden Layer）因为隐藏层的神经元不同于另外两层，通常在这个过程中肉眼不可见。隐藏层通常不止一层；这些圈圈就是节点（node），也叫神经元（neuron）；有些地方会以权重层数说这个是 2 层网络，也有些人根据节点层数说这是 3 层网络

---

激活函数

以上是神经网络的基本骨架，但是神经网络更重要的地方在于激活函数（Activation Function）。激活函数是用来最终决定面对权重计算结果神经元是否应该被激活，并且描述神经元在面对权重计算变化的结果时激活程度变化趋势的函数。其类似于开关的响应函数，或者说传递函数，把按动开关的力作为输入，开关的表现作为输出，激活函数就描述了开关（灯）在不同力下的表现情况（深度，梯度）。激活函数是神经元的特有性质。目前为止所讨论的神经网络都是线性的，也就是说整体都是采用阶跃函数作为激活函数。

试想如果神经网络不线性，激活函数如果不是阶跃的。下面就讨论了几种不同的激活函数：

sigmoid 函数